2.3 高次の導関数

• 1(1)~(5)
• 1(6)~(8)
• 2
• 3
• 4
• 5
• 6
• 7

2

(1)
は でのみ定義される 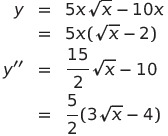であるから、 となるのは のときである
また となるのは、 のときである
増減表は下のようになる 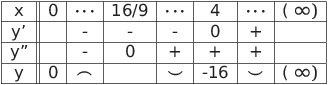よって で極小値 、 で変曲点、 で上に凸、 で下に凸
グラフの概形略

(2)
は でのみ定義される 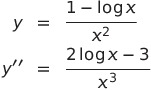であるから、 となるのは のときである
また となるのは、 のときである
増減表は下のようになる よって で極大値 、 で変曲点、 で上に凸、 で下に凸
グラフの概形略

1 連続関数

• 1.1
• 1.2
• 1.3
• 1.4

2 微分法

• 2.1
• 2.2
• 2.3
• 2.4

3 積分法

• 3.1
• 3.2
• 3.3
• 3.4

4 偏微分

• 4.1
• 4.2
• 4.3
• 4.4

5 重積分

• 5.1
• 5.2
• 5.3
• 5.4
• 5.5

6 級数

• 6.1
• 6.2

7 微分方程式

• 7.1
• 7.2