4.4 ベクトル空間の基と次元
6
(1)
![]() であるから
であるから
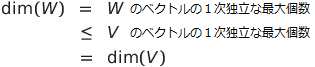
(2)
![]() の1組の基を
の1組の基を
![]() とする
とする
![]() とすると
とすると
![]() の1次独立な最大個数は
の1次独立な最大個数は
![]() であるから
であるから
![]() は1次従属である
は1次従属である
よって定理4.2.2により
![]() は
は
![]() の1次結合で書けるから
の1次結合で書けるから
![]() は
は
![]() のベクトルである
のベクトルである
よって
![]()
(1)
![]() であるから
であるから
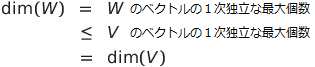
(2)
![]() の1組の基を
の1組の基を
![]() とする
とする
![]() とすると
とすると
![]() の1次独立な最大個数は
の1次独立な最大個数は
![]() であるから
であるから
![]() は1次従属である
は1次従属である
よって定理4.2.2により
![]() は
は
![]() の1次結合で書けるから
の1次結合で書けるから
![]() は
は
![]() のベクトルである
のベクトルである
よって
![]()