5.1 線形写像
3
(3)
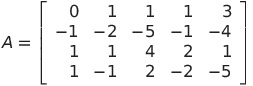 とし
とし
![]() を簡約化すると
を簡約化すると
 (i)
(i)
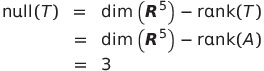
![]() のとき
のとき
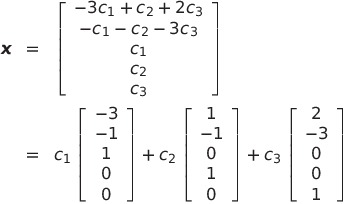 であるから、
であるから、
![]() の基として
の基として
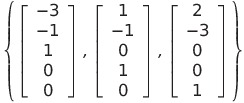 がとれる
がとれる
(ii)
![]()
![]() の1組の基は、
の1組の基は、
![]() の列ベクトルのうち1次独立な組をとればよいから
の列ベクトルのうち1次独立な組をとればよいから
![]() の基として
の基として
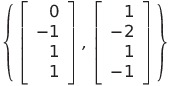 がとれる
がとれる
(3)
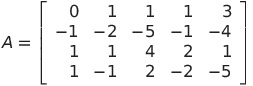 とし
とし
![]() を簡約化すると
を簡約化すると
 (i)
(i)
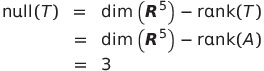
![]() のとき
のとき
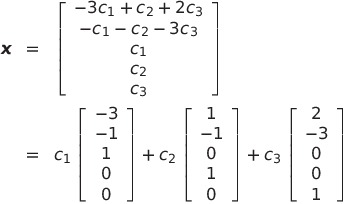 であるから、
であるから、
![]() の基として
の基として
 がとれる
がとれる
(ii)
![]()
![]() の1組の基は、
の1組の基は、
![]() の列ベクトルのうち1次独立な組をとればよいから
の列ベクトルのうち1次独立な組をとればよいから
![]() の基として
の基として
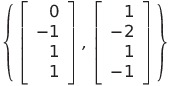 がとれる
がとれる