5.3 固有値と固有ベクトル
4
(1)
(i)
![]() の1組の基として
の1組の基として
![]() をとる。この基に関する
をとる。この基に関する
![]() の表現行列
の表現行列
![]() を求める
を求める
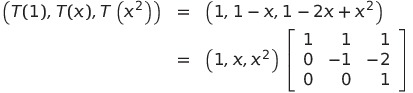 となるから
となるから
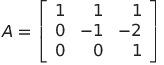 である
である
よって
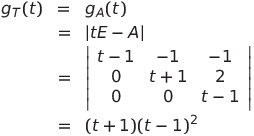 (ii)
(ii)
![]() を解いて、固有値
を解いて、固有値
![]()
(iii)
![]() とする
とする
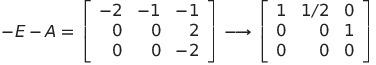 よって
よって
![]() の解は
の解は
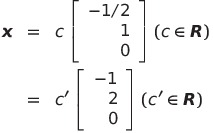 となるから
となるから
![]()
![]() とする
とする
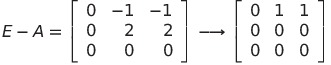 よって
よって
![]() の解は
の解は
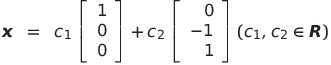 となるから
となるから
![]()
(1)
(i)
![]() の1組の基として
の1組の基として
![]() をとる。この基に関する
をとる。この基に関する
![]() の表現行列
の表現行列
![]() を求める
を求める
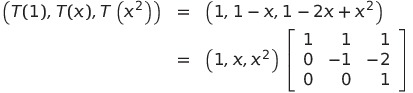 となるから
となるから
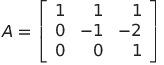 である
である
よって
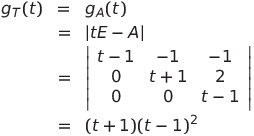 (ii)
(ii)
![]() を解いて、固有値
を解いて、固有値
![]()
(iii)
![]() とする
とする
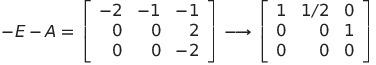 よって
よって
![]() の解は
の解は
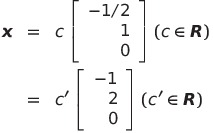 となるから
となるから
![]()
![]() とする
とする
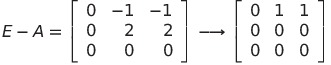 よって
よって
![]() の解は
の解は
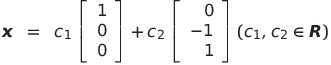 となるから
となるから
![]()