1.1 実数
2
(1)
![]() とする。
とする。
![]() のとき、
のとき、
![]() また、
また、
![]() のとき
のとき
![]() が成り立つと仮定すると、
が成り立つと仮定すると、
![]() のとき、
のとき、
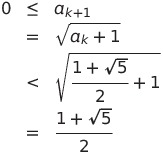 数学的帰納法より、
数学的帰納法より、
![]() であるから
であるから
![]() は有界である。
は有界である。
また
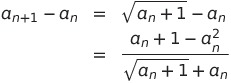 分子は
分子は
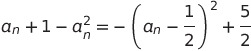 であり、
であり、![]() のとき
のとき
![]() である。
である。
また、分母は、
![]() である。
である。
よって、
![]() であるから、
であるから、
![]() は単調増加である。
は単調増加である。
![]() の極限を
の極限を
![]() とすると、有界な単調数列は収束するから、
とすると、有界な単調数列は収束するから、
![]()
![]() より、
より、
![]()
(1)
![]() とする。
とする。
![]() のとき、
のとき、
![]() また、
また、
![]() のとき
のとき
![]() が成り立つと仮定すると、
が成り立つと仮定すると、
![]() のとき、
のとき、
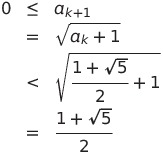 数学的帰納法より、
数学的帰納法より、
![]() であるから
であるから
![]() は有界である。
は有界である。
また
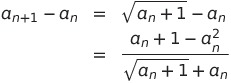 分子は
分子は
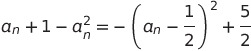 であり、
であり、![]() のとき
のとき
![]() である。
である。
また、分母は、
![]() である。
である。
よって、
![]() であるから、
であるから、
![]() は単調増加である。
は単調増加である。
![]() の極限を
の極限を
![]() とすると、有界な単調数列は収束するから、
とすると、有界な単調数列は収束するから、
![]()
![]() より、
より、
![]()