1.1 実数

• 1
• 2(1)
• 2(2)
• 3
• 4
• 5
• 6

5

(1)
とする。
ただし、,は互いに素とする。
両辺を二乗し整理すると は偶数であるから、も偶数である。
よって、整数が存在して、 これを、(*)に代入すると、 も偶数となり、,ともに約数2をもち、互いに素であることに反する。
よって、は有理数でないことが証明された。

(2)
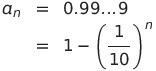とすると

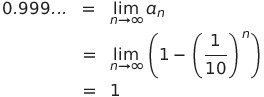
(3)
とする
の少数第位までとった少数をとすると 任意のtに対して である
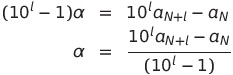
左辺の極限をとると よって は有理数であるから、は有理数である

(4)

(5)

1 連続関数

• 1.1
• 1.2
• 1.3
• 1.4

2 微分法

• 2.1
• 2.2
• 2.3
• 2.4

3 積分法

• 3.1
• 3.2
• 3.3
• 3.4

4 偏微分

• 4.1
• 4.2
• 4.3
• 4.4

5 重積分

• 5.1
• 5.2
• 5.3
• 5.4
• 5.5

6 級数

• 6.1
• 6.2

7 微分方程式

• 7.1
• 7.2