3.3 広義積分
2
p68,69の例4から例7の結果を用いている
(1)
問題になるのは
![]() が0のときである
が0のときである
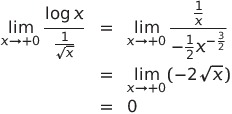 であるから、
であるから、
![]() が0に近いとき
が0に近いとき
![]() である
である
![]() が0に近いとき
が0に近いとき
![]() は収束するから、
は収束するから、
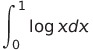 は収束する
は収束する
(2)
![]() であり、
であり、
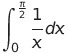 は発散するから、
は発散するから、
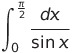 は発散する
は発散する
(3)
問題になるのは∞のときである
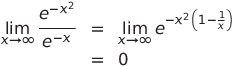 であるから
であるから
![]() が大きいとき
が大きいとき
![]() である
である
![]() が大きいとき
が大きいとき
![]() は収束するから、
は収束するから、
![]() は収束する
は収束する
(4)
問題になるのは
![]() が0と1のときである
が0と1のときである
![]() が0に近いとき
が0に近いとき
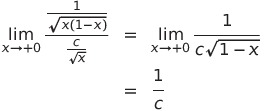 であるから
であるから
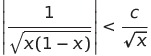 である
である
![]() が0に近いとき
が0に近いとき
![]() は収束するから
は収束するから
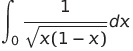 は収束する
は収束する
![]() が1に近いとき
が1に近いとき
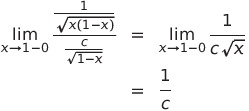 であるから
であるから
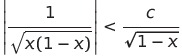 である
である
![]() が1に近いとき
が1に近いとき
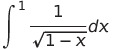 は収束するから
は収束するから
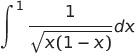 は収束する
は収束する
よって、
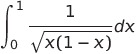 は収束する
は収束する
