3.3 広義積分
4
![]() かつ
かつ
![]() のとき
のとき
![]() は[0,1]で連続であるから積分可能である
は[0,1]で連続であるから積分可能である
![]() のとき
のとき
![]() で広義積分であり、
で広義積分であり、
![]() のとき
のとき
![]() で広義積分であるから、
で広義積分であるから、
![]() が0に近いときと
が0に近いときと
![]() が1に近いときときについて調べる
が1に近いときときについて調べる
![]() が0に近いとき
が0に近いとき
![]() である
である
![]() は
は
![]() のとき収束するから、
のとき収束するから、
![]() は収束する
は収束する
また
![]() が1に近いとき、
が1に近いとき、
![]() である
である
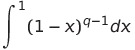 は
は
![]() のとき収束するから、
のとき収束するから、
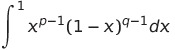 は収束する
は収束する
以上より、
![]() のとき、広義積分
のとき、広義積分
![]() は収束することが示された
は収束することが示された
![]() かつ
かつ
![]() のとき
のとき
![]() は[0,1]で連続であるから積分可能である
は[0,1]で連続であるから積分可能である
![]() のとき
のとき
![]() で広義積分であり、
で広義積分であり、
![]() のとき
のとき
![]() で広義積分であるから、
で広義積分であるから、
![]() が0に近いときと
が0に近いときと
![]() が1に近いときときについて調べる
が1に近いときときについて調べる
![]() が0に近いとき
が0に近いとき
![]() である
である
![]() は
は
![]() のとき収束するから、
のとき収束するから、
![]() は収束する
は収束する
また
![]() が1に近いとき、
が1に近いとき、
![]() である
である
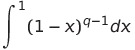 は
は
![]() のとき収束するから、
のとき収束するから、
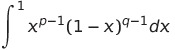 は収束する
は収束する
以上より、
![]() のとき、広義積分
のとき、広義積分
![]() は収束することが示された
は収束することが示された