4.1 多変数の関数
1
(1)
 よって、もし極限があるのならばそれは0でなければならない。
そこで
よって、もし極限があるのならばそれは0でなければならない。
そこで
![]() と0の差を評価する。
と0の差を評価する。
![]() 、
、
![]() とおくと
とおくと
![]() のとき
のとき
![]() であるから
であるから
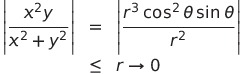 よって極限は0である
よって極限は0である
(2)
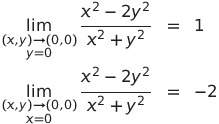 よって、2つの直線に沿った極限が異なるので、極限はない
よって、2つの直線に沿った極限が異なるので、極限はない
(3)
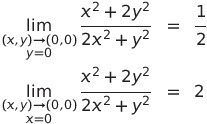 よって、2つの直線に沿った極限が異なるので、極限はない
よって、2つの直線に沿った極限が異なるので、極限はない
(1)
 よって、もし極限があるのならばそれは0でなければならない。
そこで
よって、もし極限があるのならばそれは0でなければならない。
そこで
![]() と0の差を評価する。
と0の差を評価する。
![]() 、
、
![]() とおくと
とおくと
![]() のとき
のとき
![]() であるから
であるから
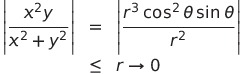 よって極限は0である
よって極限は0である
(2)
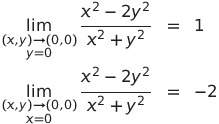 よって、2つの直線に沿った極限が異なるので、極限はない
よって、2つの直線に沿った極限が異なるので、極限はない
(3)
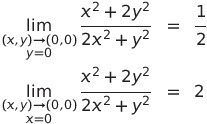 よって、2つの直線に沿った極限が異なるので、極限はない
よって、2つの直線に沿った極限が異なるので、極限はない