4.2 1次独立と1次従属
1
(1)
与えられたベクトルの1次関係を
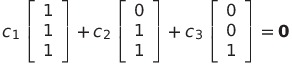 とすると
とすると
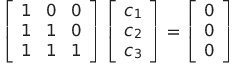 となる
となる
これを解くと
![]() となるから1次独立である
となるから1次独立である
(2)
与えられたベクトルの1次関係を
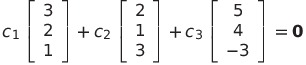 とすると
とすると
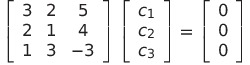 となる
となる
これを解くと自明でない解が存在するので、1次従属である
(3)
与えられたベクトルの1次関係を
 とすると
とすると
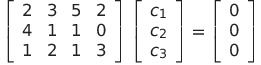 となる
となる
これを解くと自明でない解が存在するので、1次従属である
(4)
与えられたベクトルの1次関係を
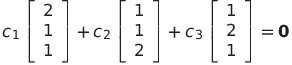 とすると
とすると
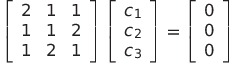 となる
となる
これを解くと
![]() となるから1次独立である
となるから1次独立である
(5)
与えられたベクトルの1次関係を
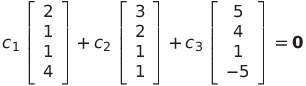 とすると
とすると
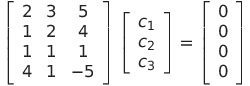 となる
となる
これを解くと自明でない解が存在するので、1次従属である
(6)
与えられたベクトルの1次関係を
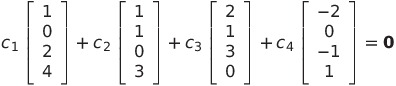 とすると
とすると
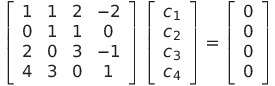 となる
となる
これを解くと
![]() となるから1次独立である
となるから1次独立である
(7)
与えられたベクトルを
![]() 、
、
![]() 、
、
![]() とすると、与えられたベクトルの1次関係は
とすると、与えられたベクトルの1次関係は
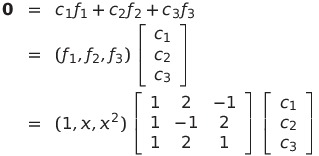 となる
となる
1、
![]() 、
、
![]() は1次独立だから定理4.2.4より
は1次独立だから定理4.2.4より
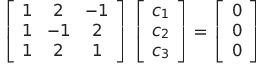 である
である
これを解いて
![]() となるから
となるから
![]() 、
、
![]() 、
、
![]() は1次独立である
は1次独立である
