4.4 陰関数の定理

• 1
• 2
• 3
• 4
• 5
• 6(1)
• 6(2)
• 7(1)
• 7(2)

6

(1)
とする
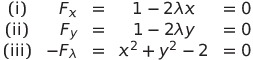
とおくと とすると、(i)と(ii)を満たさないため
よって、(i)より また(ii)より これを(iii)に代入すると となり、 、すなわち （複合同順）となる
この２点が が条件付きの極値をとる候補である
点 の近くでの の陰関数を とおき、 とおく
を で繰り返し微分すると であるから また、 であるから よって であるから、 は で極小値をとる すなわち は条件 の下に点 で極小値－２をとる
また の近くでの の陰関数を とし、 とおくと、同様にして であるから よって点 で極大値２をとる

1 連続関数

• 1.1
• 1.2
• 1.3
• 1.4

2 微分法

• 2.1
• 2.2
• 2.3
• 2.4

3 積分法

• 3.1
• 3.2
• 3.3
• 3.4

4 偏微分

• 4.1
• 4.2
• 4.3
• 4.4

5 重積分

• 5.1
• 5.2
• 5.3
• 5.4
• 5.5

6 級数

• 6.1
• 6.2

7 微分方程式

• 7.1
• 7.2