4.4 陰関数の定理
7
ラグランジュの未定乗数法によって求められる極値は、最大値・最小値の候補でしかないが、有界閉集合の場合には、候補点が最大・最小点を表していると考えてよい。
(2)
![]() のときを考える
のときを考える
![]() を解くと
を解くと
![]() これは
これは
![]() を満たす
を満たす
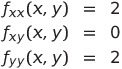 であるから
であるから
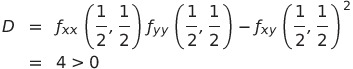
![]() よって、
よって、
![]() は
は
![]() において極小値
において極小値
![]() をとる
をとる
次に
![]() のときを考える
のときを考える
![]() とする
とする
![]() とおくと
とおくと
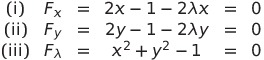
![]() とすると、(i)(ii)を満たさないため
とすると、(i)(ii)を満たさないため
![]()
よって(i)(ii)より
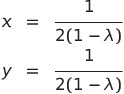 (iii)に代入して整理すると
(iii)に代入して整理すると
![]() であるから
であるから
![]()
よって
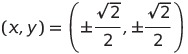 (複合同順)
(複合同順)
この2点が
![]() が条件付きで極値をとる候補である
が条件付きで極値をとる候補である
点
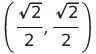 の近くでの
の近くでの
![]() の陰関数を
の陰関数を
![]() とおき
とおき
![]() とおく
とおく
![]() を
を
![]() で繰り返し微分すると
で繰り返し微分すると
![]()
![]() よって
よって
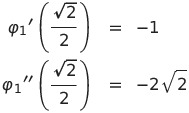 である
である
![]() であるから
であるから
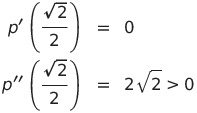 よって点
よって点
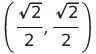 で極小値
で極小値
![]() をとる
をとる
同様に
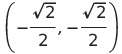 では、
では、
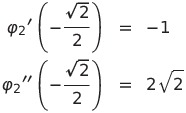 であるから
であるから
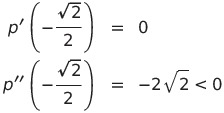 よって点
よって点
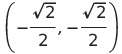 で極大値
で極大値
![]() をとる
をとる
![]() は有界閉集合で、この上で
は有界閉集合で、この上で
![]() は連続だから、
は連続だから、
![]() において最小値
において最小値
![]()
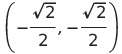 において最大値
において最大値
![]() をとる
をとる
