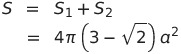5.4 重積分の応用（体積と曲面積）

• 1(1)
• 1(2)
• 1(3)(4)
• 1(5)
• 2
• 3
• 4(1)(2)
• 4(3)(4)
• 4(5)
• 5(1)(2)
• 5(3)(4)

4

(1)
とおく
図形の対称性から、円柱面の上部で、 の上にある部分を計算して8倍すればよい
円柱の方程式の両辺を、 および で偏微分すると、 、 となるから
、
よって

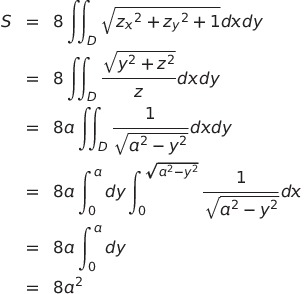
(2)
求める曲面積は、円柱表面上の部分と球面上の部分に分けられ、それぞれを 、 とする
円柱表面上の部分は、円柱の側面積を考えればよいから、 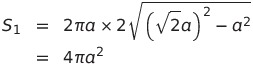また、球面上の部分は、 とおくと、図形の対称性から球面の上部で、 の上にある部分を計算して8倍すればよいから 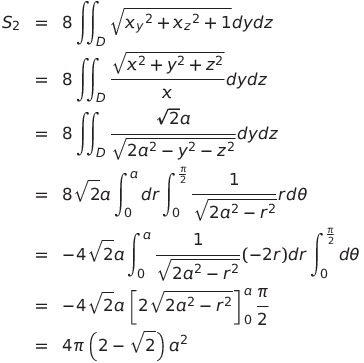よって

1 連続関数

• 1.1
• 1.2
• 1.3
• 1.4

2 微分法

• 2.1
• 2.2
• 2.3
• 2.4

3 積分法

• 3.1
• 3.2
• 3.3
• 3.4

4 偏微分

• 4.1
• 4.2
• 4.3
• 4.4

5 重積分

• 5.1
• 5.2
• 5.3
• 5.4
• 5.5

6 級数

• 6.1
• 6.2

7 微分方程式

• 7.1
• 7.2